以太坊 PoS 共识协议详解(二):Casper FFG
本文是介绍以太坊 PoS 共识协议的第二部分,主要对最终性工具 Casper FFG 进行全面说明。
许多文章都介绍过 Casper FFG 的运行机制,但很少解释这些机制为什么有效。希望本文能为读者理解 Casper FFG 的有效性提供一些参考。
总体而言,Casper FFG 的机制并不复杂,其有效性主要归功于为两个重要理念:两阶段提交,以及可问责安全性。
两阶段提交赋予了 Casper FFG 经典的共识安全性,令其能够声明区块是最终化的,并确信诚实验证者永远不会回滚最终化的区块。但两阶段提交生效的条件是诚实验证者控制至少三分之二的质押权益。因此,针对作恶验证者超过三分之一的情况,Casper FFG 还提供了可问责安全性作为额外的保障。如果链上出现最终性冲突,至少三分之一的总质押权益会经由罚没作恶验证者被销毁。
概述
Casper FFG 是一种元共识协议。可以作为覆盖层运行在底层共识协议之上,为其添加最终性。回顾一下,最终性是保证链中的一些区块永远不会被回滚的属性。在以太坊的权益证明共识中,底层协议 LMD GHOST 并不提供最终性,验证者构建竞争链不会受到惩罚。Casper FFG 的作用就是作为“最终性小工具 (finality gadget) ”来为 LMD GHOST 添加最终性。
Casper FFG 利用了权益证明协议的性质:参与者是已知的(管理质押以太坊的验证者)。因此,可以通过计数来判断是否获得多数诚实验证者的投票(确切地说是管理多数质押权益的验证者的投票,每个验证者的投票都会根据其管理的权益价值被加权,简单起见,这一点后文不再赘述)。
协议在异步网络 (Internet) 上运行,这意味着如果想同时实现安全性和活性,最多只能容忍 $\frac{1}{3}$ 的验证者存在恶意或故障。这是共识理论中的一个著名结论,推理如下:
- 设共有 $n$ 个验证者,其中 $f$ 个可能以某种方式存在故障或恶意。
- 为了保持活性,协议需要在只收到 $n-f$ 个验证者的响应后就能做出决定,因为那 $f$ 个验证者可能无法或拒绝进行投票。
- 但由于是异步环境,所以未收到的 $f$ 个响应可能只是延迟了,并非故障导致。
- 因此,必须考虑在收到的 $n-f$ 个响应中,最多可能有 $f$ 个来自有故障或恶意验证者。
- 为了保证在收到 $n-f$ 个验证者响应后诚实验证者的仍占多数,则需要 $\frac{(n-f)}{2} > f$,即 $f <\frac{n}{3}$。
总之,与所有经典拜占庭容错 (BFT) 协议一样,Casper FFG 在不到三分之一的验证者集存在故障或恶意时,能够提供最终性。而特别之处在于,即使超过三分之一的验证者存在故障或恶意行为,Casper FFG 仍能够提供经济最终性(可问责安全性)。
本文将单独考虑 Casper FFG,不会过多花费时间讨论其如何与 LMD GHOST 集成。Casper FFG 论文也几乎没有涉及到底层区块链共识机制。后续文章将继续探讨两者是如何结合为 Gasper 的。
命名
Casper FFG 协议的名称由两部分组成:
Casper
协议名中的 Casper 部分似乎出自 Vlad Zamfir 之手。正如他在《History of Casper》Part 5 中解释的:
在本章中,我将讲述 Casper 协议的诞生,它是将 Aviv Zohar 和 Jonatan Sompolinsky 的 GHOST 协议应用于权益证明机制之上的产物。 我称之为“友好的幽灵”,因为其激励机制旨在对抗寡头垄断的审查制度:这些激励机制迫使卡特尔对非卡特尔验证者保持友好。
这里提到的 GHOST 协议就是在前一篇文章中介绍过的协议。Casper 这个名字其实来自 Casper the Friendly Ghost,是一个自 1940 年代以来就存在的卡通角色。
Zamfir 最初将协议命名为 Casper TFG(The Friendly Ghost,友好的幽灵),后来又改名为 Casper CBC(Correct By Construction,通过构建实现正确性)。Vitalik 的 Casper FFG 与 Zamfir 的 Casper TFG/CBC 几乎同时出现,但两者并没有什么共同之处,Casper FFG 也没有使用 GHOST 协议。
FFG
如 Casper FFG 论文标题所写,FFG 代表“Friendly Finality Gadget(友好的最终性小工具)”。这一命名在借鉴了 Zamfir 的 TFG 的同时,也表明了 Casper FFG 不是一个完全独立的区块链协议,而是一个可以添加到底层共识协议中实现最终性的“小工具”。
术语
Epoch 和检查点
为了就最终性做出决定,Casper FFG 机制需要处理来自至少 $\frac{2}{3}$ 的验证者集的投票。在以太坊中,验证者集非常庞大,成千上万个验证者的投票同时广播、传播和处理是不现实的。
为了解决这个问题,投票会分散在 Epoch 的持续时间内进行1,在 Eth2 中,一个 Epoch 由 32 个间隔 12 秒的 Slot 组成。在每个 Slot 中,总验证者集合的 $\frac{2}{3}$ 会被安排广播投票,因此每个验证者在每个 Epoch 会投票一次。实现中为了提高效率将每个验证者的 Casper FFG 投票与其 LMD GHOST 投票绑定在一起,但不是必须如此。
为了确保在不同时间投票的验证者拥有共同的投票对象,我们令其对检查点 (Checkpoint) 进行投票,检查点是 Epoch 的第一个 Slot。第 $N$ 个 Epoch 的检查点位于第 $32N$ 个 Slot(Slot 和 Epoch 的编号从 0 开始)。
 一个 Epoch 分为 32 个 Slot,每个 Slot 通常包含一个区块。每个 Epoch 的第一个 Slot 是其检查点
一个 Epoch 分为 32 个 Slot,每个 Slot 通常包含一个区块。每个 Epoch 的第一个 Slot 是其检查点
“最终化 Epoch”这种表述是不正确的,Casper FFG 最终化的是检查点。当完成第 $N$ 个 Epoch 的检查点最终化时,也就最终化了含第 $32N$ 个 Slot 在内的所有内容,包括整个第 $N-1$ 个 Epoch 和第 $N$ 个 Epoch 的第一个 Slot。但第 $N$ 个 Epoch 并没有完成最终化,还有 31 个 Slot 未最终化。
暂且假设每个 Slot 都包含一个区块,因为原始的 Casper FFG 检查点是基于区块高度而不是 Slot 号的。在协议中,一个检查点对象只包含其 Epoch 编号以及 Epoch 第一个 Slot 中区块的哈希根 (root):
1
2
3
class Checkpoint(Container):
epoch: Epoch
root: Root
合理化和最终化
与经典的 BFT 共识协议类似,Casper FFG 通过两轮流程(合理化 Justification,最终化 Finalization)来实现最终性。
第一轮:我向网络广播对当前 Epoch 的检查点的看法(记为 $X$),并获取其他人的看法。如果绝大多数验证者也支持 $X$,那么我就可以对 $X$ 进行合理化。合理化仅限于我的网络视图:在这一阶段,我相信网络中的大多数验证者都认为 $X$ 对最终化有利。但是我还不知道网络上的其他人是否也得出了同样的结论。在对抗性条件下,可能有足够多的其他验证者无法就 $X$ 做出决定。
第二轮:我广播“我接收到的绝大多数验证者支持 $X$” 的消息(即,“我已经合理化了 $X$”),并询问其他验证者是否认为绝大多数验证者支持 $X$(即,他们是否已经合理化 $X$)。如果绝大多数验证者同意 $X$ 是合理的,那么我将最终化 $X$。最终化是全局属性:一旦一个检查点被最终化,任何诚实的验证者都不会将其回滚。即使其他验证者还没有在其视图中将该检查点标记为最终化,我也知道他们至少将其标记为了已合理化,并且没有任何(不可惩罚的)行为能够撤销该合理化。
总结一下,我要确定整个网络都同意不会回滚某个区块,需要以下步骤2:
第一轮(理想情况下可合理化)
a. 我告诉网络我支持的检查点。
b. 我从网络中获取其他验证者支持的检查点。
c. 如果 $\frac{2}{3}$ 的验证者与我意见相同,我将合理化该检查点。
第二轮(理想情况下可最终化)
a. 我将我已合理化的检查点告诉网络。
b. 我从网络中获取其他验证者已合理化的检查点。
c. 如果 $\frac{2}{3}$ 的验证者与我意见相同,我将最终化该检查点。
简而言之,当我合理化一个检查点时,我承诺永远不回滚它。当我最终化一个检查点时,我知道所有诚实验证者都承诺永远不回滚它。
在理想条件下,每轮持续一个 Epoch,因此合理化检查点需要一个 Epoch,最终化检查点需要再花费一个 Epoch。
- 在 Epoch N 开始时,我们的目标是合理化检查点$N-1$ 并最终化检查点$N-2$。
- 具体来说,协议中最终化一个检查点需要 12.8 分钟,即两个 Epoch。在 Casper FFG 中,这两轮是重叠流水线式的,因此尽管最终化一个检查点总共需要 12.8 分钟,但仍然可以做到每隔 6.4 分钟(即每个 Epoch)最终化一个检查点。
- 注意,在协议外部,如果不存在长链重组,则可以稍早于 12.8 分钟预见到某个检查点可能被最终化。例如可能在第二轮进行到 $\frac{2}{3}$ 的时候(大约 11 分钟)就收集了足够多的来自 $\frac{2}{3}$ 验证者的投票。但协议内部的合理化和最终化仅在 Epoch 结束处理期间进行。
源和目标 链接和冲突
Casper FFG 中的投票包含两个部分:源 (Source) 检查点投票和目标 (Target) 检查点投票,即见证数据中的 source 和 target 字段:
1
2
3
4
5
6
7
8
class AttestationData(Container):
slot: Slot
index: CommitteeIndex
# LMD GHOST vote
beacon_block_root: Root
# FFG vote
source: Checkpoint
target: Checkpoint
源和目标投票同时以链接 (Link) 的形式进行广播:$𝑠→𝑡$,其中 $s$ 是源检查点,$t$ 是目标检查点。
目标投票的作用是广播验证者视图中下一个应该被合理化的检查点,是验证者的第一轮投票。目标投票对不会滚该检查点的软(条件性的)承诺,条件是收到 $\frac{2}{3}$ 的验证者对该检查点的承诺。
源投票的作用是广播验证者已经收到网络中 $\frac{2}{3}$ 的验证者支持检查点$s$,且 $s$ 是已知符合该条件的最新检查点,是验证者的第二轮投票。通过源投票,验证者将之前不回滚检查点的软承诺升级为永远不回滚的硬(无条件)承诺。
诚实验证者的源投票始终是其链视图中最高的已合理化检查点。其目标投票将是当前 Epoch 的检查点,该检查点是源检查点的后代。源和目标检查点不必连续,跳过检查点是允许的。但是,当信标链运行平稳时,一个 Epoch 的目标投票将是下一个 Epoch 的源投票。
 从已合理化检查点到其后代链上检查点的链接是有效的。图中只展示了检查点,中间的区块被省略
从已合理化检查点到其后代链上检查点的链接是有效的。图中只展示了检查点,中间的区块被省略
在有效的链接中,源检查点始终是目标检查点的祖先。否则,验证者会自相矛盾:源投票承诺了永远不会回滚检查点 $s$, 如果目标检查点 $t$ 不是 $s$ 的后代,那么实际上就是在投票回滚 $s$。但发布这样的无效链接并不算可罚没的违规行为。
 从已合理化检查点到非其后代链上的检查点的链接是无效的。这两个检查点是冲突的,因为它们都不是彼此的祖先
从已合理化检查点到非其后代链上的检查点的链接是无效的。这两个检查点是冲突的,因为它们都不是彼此的祖先
评估 Casper FFG 投票时,只会考虑在区块中接收到的投票。与 LMD GHOST 的分叉选择不同,验证者不会考虑通过 Gossip 或任何其他方式接收到的 Casper FFG 投票。因为我们围绕最终性的决策必须有一个共同记录,而区块历史正是这样的共同记录。因此,前文提到“告诉网络”时,实际上是说验证者广播了一个见证,该见证将被区块提议者拾取并包含在了一个区块中。当提到“从网络获取”时,实际上是说验证者处理了包含在区块中的见证。
绝对多数链接
如上所述,链接是一个 Casper FFG 投票对,用于链接源检查点和目标检查点,$s→t$。
当超过 $\frac{2}{3}$ 的验证者(按权益加权)发布了相同的链接(且其投票被及时包含在区块中)时,链接 $s→t$ 就是一个绝对多数链接 (Supermajority Link)。
Casper FFG 的机制
在了解了大部分术语和关键概念之后,本节将详细介绍 Casper FFG 的运行方式。
合理化
当节点看到从已合理化检查点 $c_1$ 到检查点 $c_2$ 的绝对多数链接时,就认为检查点 $c_2$ 是已合理化的。
 节点已经看到绝对多数链接 $C_N→C_{N+2}$ ,因此将 $C_{N+2}$ 标记为已合理化。已合理化的检查点用阴影线标记并标有“J”
节点已经看到绝对多数链接 $C_N→C_{N+2}$ ,因此将 $C_{N+2}$ 标记为已合理化。已合理化的检查点用阴影线标记并标有“J”
合理化意味着我已经看到超过 $\frac{2}{3}$ 的验证者集做出承诺不会回滚检查点 $c_2$,其条件是收到至少 $\frac{2}{3}$ 同样承诺不回滚 $c_2$ 的验证者的确认。换句话说,如果一个验证者看到超过 $\frac{2}{3}$ 的其他验证者承诺不回滚检查点$c_2$,那么该验证者本身也承诺不会回滚 $c_2$。
最终化
当节点看到从已合理化检查点 $c_1$ 到检查点 $c_2$ 的绝对多数链接,且检查点 $c_2$ 是 $c_1$ 的直接子检查点时,就会认为检查点 $c_1$ 是最终化的。
换句话说,当一个已合理化检查点的直接子级也已合理化时,该检查点成为最终化的检查点。
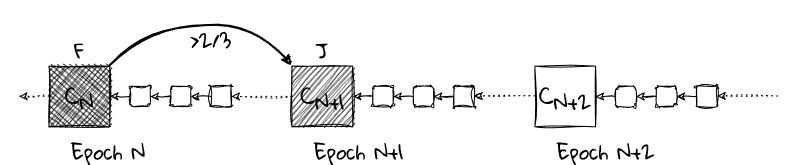 节点已经看到绝对多数链接 $C_N → C_{N+1}$,因此将 $C_{N+1}$ 标记为已合理化。由于 $C_{N+1}$ 是检查点树中 $C_N$ 的直接子级,因而将 $C_N$ 标记为最终化。最终化的检查点用交叉阴影线标记并标有“F”
节点已经看到绝对多数链接 $C_N → C_{N+1}$,因此将 $C_{N+1}$ 标记为已合理化。由于 $C_{N+1}$ 是检查点树中 $C_N$ 的直接子级,因而将 $C_N$ 标记为最终化。最终化的检查点用交叉阴影线标记并标有“F”
最终化意味着我已经看到超过 $\frac{2}{3}$ 的验证者确认其已收到超过 $\frac{2}{3}$ 的验证者的承诺,因此不会回滚检查点 $c_1$。此时检查点 $c_1$ 已经不可能被回滚,除非至少有 $\frac{1}{3}$ 的验证者被证明反悔,并因此受到罚没。
Casper 守则
在 Casper FFG 论文中,为检查点定义了高度:如果 $c$ 是一个检查点,那么 $h(c)$ 就是该检查点的高度。检查点高度随距创世块的距离单调增加。
在 Eth2 的 Casper FFG 实现中,检查点高度是检查点的 Epoch 编号:$h(c) = c.epoch$。前文提到,检查点包含区块哈希和 Epoch 编号这两个部分。如果这两部分中有任何一个不同,那么检查点就是不同的。
Casper FFG 的可问责安全证明依赖于任何违反以下两条规定(或“惩罚守则”)的验证者都会受到罚没。
禁止双重投票
守则 1:验证者不得发布不同的投票 $s_1 → t_1$ 和 $s_2 → t_2$,使得 $h(t_1) = h(t_2)$。
简单来说,验证者对任意目标 Epoch 只能进行最多一次投票。
 违反守则 1 的一种方式:使用不同的源检查点投票给相同的目标检查点:$0 → 3$ 和 $1 → 3$
违反守则 1 的一种方式:使用不同的源检查点投票给相同的目标检查点:$0 → 3$ 和 $1 → 3$
 违反守则 1 的另一种方式:在同一个 Epoch 中投票给不同的目标检查点:$0 → 3$ 和 $0 → 3’$
违反守则 1 的另一种方式:在同一个 Epoch 中投票给不同的目标检查点:$0 → 3$ 和 $0 → 3’$
禁止包围投票
守则 2:验证者不得发布不同的投票 $s_1 → t_1$ 和 $s_2 → t_2$,使得使得 $h(s_1) < h(s_2) < h(t_2) < h(t_1)$。
也就是说,验证者不得发布投票,使其链接包围或被其先前投票的链接包围。
 违反守则 2 的一种方式:链接 $0 → 3$ 包围链接 $1 → 2$
违反守则 2 的一种方式:链接 $0 → 3$ 包围链接 $1 → 2$
 违反守则 2 的另一种方式:仍是链接 $0 → 3$ 包围链接 $1 → 2$,但处于不同分支
违反守则 2 的另一种方式:仍是链接 $0 → 3$ 包围链接 $1 → 2$,但处于不同分支
罚没机制
任何违反 Casper 守则之一的验证者都将被罚没 (Slash)。这意味着其部分或全部质押权益将被扣除,并会被踢出验证者集。
罚没机制让不良行为 (是可能导致冲突检查点最终化的行为)有了代价,是 Casper 可问责安全保证的基础。
从协议内部检测违规行为比较困难,尤其检测包围投票可能需要搜索验证者大量的历史投票记录。因此,实现中依赖外部罚没检测服务3 来检测违规行为并将证据提交给区块提议者。验证者会对其发布的每个见证进行签名,因此,给定两个相互冲突的证明,只需验证其签名并证明验证者在发布时违反了守则即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def process_attester_slashing(state: BeaconState, attester_slashing: AttesterSlashing) -> None:
attestation_1 = attester_slashing.attestation_1
attestation_2 = attester_slashing.attestation_2
assert is_slashable_attestation_data(attestation_1.data, attestation_2.data)
assert is_valid_indexed_attestation(state, attestation_1)
assert is_valid_indexed_attestation(state, attestation_2)
slashed_any = False
indices = set(attestation_1.attesting_indices).intersection(attestation_2.attesting_indices)
for index in sorted(indices):
if is_slashable_validator(state.validators[index], get_current_epoch(state)):
slash_validator(state, index)
slashed_any = True
assert slashed_any
Casper FFG 论文中描述的协议假设,一旦证明违反了罚没条件,“验证者的全部存款将被没收”。Eth2 实现了该假设的一种变体,根据给定周期内被罚没的总权益比例来调整验证者的罚没比例。如果在 36 天的窗口期内,$\frac{1}{3}$ 的总质押权益违反了罚没条件,那么违规者的所有权益都会被没收,与经典 Casper FFG 协议的假设一致。但如果窗口期内的总罚没很少,那么违规者几乎不会被没收权益。这种细微调整在实践中并不影响 Casper FFG 的保证,至少自信标链 Bellatrix 升级将 PROPORTIONAL_SLASHING_MULTIPLIER 常量设置为最终值以来如此。
分叉选择规则
Casper FFG 的分叉选择规则是对底层共识机制的分叉选择规则的修改。根据 Casper FFG 论文,底层共识机制必须:
遵循包含最高合理化检查点的链
纯粹的 LMD GHOST 协议总会从创世块开始搜索链头区块。当被 Casper FFG 的分叉选择规则修改后,LMD GHOST 将从其已知的最高合理化检查点开始搜索链头,并忽略所有不属于最高合理化检查点子链的潜在链头区块。后续文章在讨论 Gasper 时会更详细地介绍这点。
正是对底层共识协议分叉选择规则的这种修改赋予了其最终性。当节点在其本地视图中合理化一个检查点时,就承诺了永远不会回滚它。因此,底层链必须始终包含该检查点;所有不包含该检查点的分支都必须被忽略。
需要注意的是,这种分叉选择规则与 Casper FFG 的可信赖活性保证是兼容的。
Casper FFG 的保证
Casper FFG 共识协议提供了两种与经典共识协议中的安全性和活性相类似但又不同的保证:可问责安全性 (Accountable Safety) 和可信赖活性 (Plausible Liveness)。
可问责安全性
经典的 PBFT 共识协议只能在不到三分之一的验证者作恶的情况下保证安全性。
Casper FFG 在少于三分之一权益的验证者作恶的情况下,本质上提供了相同的安全保证:最终化的检查点将永远不会被回滚。此外,Casper FFG 还提供了额外的保证,即如果冲突的检查点最终化,那么代表至少三分之一质押以太坊的验证者将被罚没。 这被称为“可问责安全性”,因为我们可以准确识别哪些验证者行为不当并直接对其进行惩罚。
这一额外的安全性保证并非并非通常意义上共识协议所指的安全性,而是具有加密经济学特性的安全性:不当行为会受到协议极强的反激励。通常被称为“经济最终性”。
证明
Casper FFG 可问责安全性的证明相当直观。这里将大致按照 Casper FFG 论文中的方式勾勒出证明过程,但会使用 Epoch 代替论文中更抽象的”检查点高度”。
我们要证明的是:如果少于 $\frac{1}{3}$ 的验证者(按权益加权)违反 Casper 守则,则两个冲突的检查点不能同时最终化。
证明的思路是:证明最终化冲突检查点的唯一方式,是使一个绝对多数链接被另一个绝对多数链接包围,而这与命题中的假设相矛盾,包围投票是违反第二守则的。
显然,在这一假设下,任意 Epoch 中最多只能有一个检查点被合理化。这是由禁止重复投票守则直接得出的。
取 Epoch $m$ 和 $n$ 中的两个冲突的最终化检查点 $a_m$ 和 $b_n$。由于相互冲突,所以两检查点彼此都不是对方的后代。由上述观察可知,$m ≠ n$。在不失一般性的条件下,取 $m < n$,则 $b_n$ 是更高的最终化检查点。
一定存在一系列连续的已合理化检查点,从根检查点一直连到 $b_n$,且相互之间具有绝对多数链接。也就是存在一组 $k$ 个绝对多数链接 $\lbrace r → b_{i_1}, b_{i_1} → b_{i_2}, b_{i_2} → b_{i_3}, \dots, b_{i_k-1} → b_{i_k}\rbrace$,其中 $i_k = n$,这是由合理化的定义得到的。因此,导向 $b_n$ 的已合理化检查点集是 $B = \lbrace r, b_{i_1}, b_{i_2}, b_{i_3}, \dots, b_{i_k-1}, b_{i_k}\rbrace$。
 对于任意最终化检查点,例如 $b_{10}$,都存在一条由绝对多数链接组成的连续链,从根检查点 $r$ 一直连到它。这里的链接链合理化了检查点集 $B = \lbrace r, b_1, b_4, b_5, b_9, b_{10}\rbrace$ 阴影线表示检查点是合理化的(也可能最终化);交叉阴影线表示检查点是最终化的(并标记“F”)
对于任意最终化检查点,例如 $b_{10}$,都存在一条由绝对多数链接组成的连续链,从根检查点 $r$ 一直连到它。这里的链接链合理化了检查点集 $B = \lbrace r, b_1, b_4, b_5, b_9, b_{10}\rbrace$ 阴影线表示检查点是合理化的(也可能最终化);交叉阴影线表示检查点是最终化的(并标记“F”)
考虑冲突的最终化检查点 $a_m$。根据最终化的定义,从 $a_m$ 到下一个 Epoch 的 $a_{m+1}$,必然存在绝对多数链接 $a_m → a_{m+1}$ 。显然,$a_m$ 和 $a_{m+1}$ 都不在集合 $B$ 中,且集合 $B$ 不包含检查点 $b_m$ 或 $b_{m+1}$,因为一个 Epoch 中最多只能有一个合理化检查点。
因此,检查点对 $(a_m, a_{m+1})$ 必定落在集合 $B$ 的两个连续元素的 Epoch 之间,设为 $b_{i_{j-1}}$ 和 $b_{i_j}$。即存在一个 $j$ 满足 $i_{j-1} < m < m+1 < i_j$。
由此可见,必定存在绝对多数链接 $b_{i_{j-1}} → b_{i_j}$ 包围了绝对多数链接 $a_m → a_{m+1}$ 。包围链接和被包围链接都需要至少 $\frac{1}{3}$ 的验证者违背 Casper 第二守则才可能存在,与假设不符。
 假设较早的冲突检查点 $a_6$ 最终化,则必然存在绝对多数链接 $a_6 → a_7$。$b$ 链上必然存在一条绝对多数链接(本例中为 $b_5 → b_9$) 跨越 $a_6 → a_7$
假设较早的冲突检查点 $a_6$ 最终化,则必然存在绝对多数链接 $a_6 → a_7$。$b$ 链上必然存在一条绝对多数链接(本例中为 $b_5 → b_9$) 跨越 $a_6 → a_7$
这样就用反证法证明了,如果少于 $\frac{1}{3}$ 的验证者(按权益加权)违反 Casper 守则,则两个冲突的检查点不能同时最终化。
为什么是三分之二?
最终化的阈值设定在 $\frac{2}{3}$ 的原因其实并不像直观感觉上那么简单。注意,这里 $\frac{2}{3}$ 的含义是总质押权益的 $\frac{2}{3}$ ,与本文开头介绍的 PBFT 算法中共识生效的阈值含义并不相同。实际上绝对多数链接的定义可以选取任意大于 $\frac{1}{2}$ 的值作为阈值。设此阈值为 $p$:若验证者集中比例为 $p$ 的验证者投票最终化一个检查点,则该检查点被最终化。
该值的设定实际是要平衡两个因素:
- 从活性角度看,协议的容错度为 $1-p$(多于 $1-p$ 的验证者不响应就无法达到 $p$);
- 从安全性角度看,协议的容错度为 $2p-1$(最终化两个冲突检查点各需要 $p$,两者重复的部分为 $2p-1$)。
令 $1-p = 2p-1$ 得 $p=\frac{2}{3}$ 。因此,将 $p$ 设置为 $\frac{2}{3}$ 可以最大限度地提高对活性攻击的容错性(不到三分之一的作恶权益无法妨碍最终化),同时最大限度地提高对安全故障的容错性(如果最终化冲突检查点,至少三分之一的质押权益将被罚没)。
经济最终性
可问责安全性的证明依赖于以下两个条件:
- 不存在指向相同高度不同检查点的绝对多数链接。
- 不存在互相包围的绝对多数链接。
这两个条件由两条 Casper 守则强制达成。任何违反守则的验证者都会被罚没,因此,在发生冲突最终化的情况下,可以保证至少 $\frac{1}{3}$ 的质押以太坊被罚没。
罚没机制使对链的攻击需要付出代价,成功攻击的成本巨大4。正如 Vitalik 所说:
如果一个区块被最终化,那么它就成为了链的一部分,改变它会非常昂贵。
我们称之为“经济最终性 (Economic Finality) ”,因为最终性不是由软件而是由攻击成本保障的。验证者的质押权益是“正当行为保证金”,如果被证明违反了协议规则,就可以没收其权益。
那么为什么需要经济最终性这一概念呢?经典 PBFT 并不依赖这样的结构来实现最终性。协议难道不能直接拒绝最终化冲突的检查点吗?
区别在于 PBFT 可以奢侈地假设作恶验证者不到三分之一。在 Casper FFG 中,持有不到三分之一权益的攻击者同样无法最终化冲突的检查点。然而,在无许可区块链中,必须有防御措施来应对作恶权益超过三分之一的情况。而罚没机制就是这一防御措施,为协议提供了经济最终性保证:如果超过三分之一的验证者行为不当,虽然无法阻止其最终化冲突检查点,但可以令其付出巨大的代价。
Vitalik 在一篇博文(论结算最终性)中说道:
我们不能保证“X 永远不会被回滚”,但我们可以保证稍弱的声明:“要么 X 永远不会被回滚,要么一大群验证者将自愿销毁自己的数百万美元的资产”。
面对超过三分之一的攻击者和异步网络,验证者仅仅在协议内拒绝最终化冲突检查点是没有意义的。能够最终化冲突检查点的攻击依赖于将诚实验证者集分割开来,使其看不到彼此的投票,也不知道对方最终化的对象。经济最终性是应对这一强大攻击威胁的有力安全保证。在发生冲突最终化的情况下,最终的补救措施是人工干预。正如 Vitalik 在同一篇文章中所说:“围绕链上资产的用户社区可以用常识来区分哪个分叉不是攻击,而真正代表了最初被一致同意最终化的交易的结果”。
可信赖活性
Casper FFG 本身并不提供经典意义上的活性,即确保用户的交易被包含在链上。所有区块生产和链构建都由底层共识机制 (LMD GHOST) 负责。
但我们希望 Casper FFG 在某种程度上具备活性:只要至少三分之二的验证者是诚实的,我们就希望能继续合理化并最终化检查点,且不会导致任何诚实验证者被罚没。反过来,我们永远不希望陷入“除非罚没诚实验证者否则就无法最终化新检查点”的僵局。这也符合“终会发生好事”的活性定义。用 Vitalik 的话来说:
可信赖活性基本上意味着“算法不应该被‘卡住’,无法最终化任何东西”。
用 Casper 论文中的表述就是:
只要存在扩展最终化链的子链,就始终能通过绝对多数链接来生成新的最终化检查点。
证明过程如下:设存在一个最高合理化检查点 $a$,且存在一个位于相同或更高高度的检查点 $b$(不一定是 $a$ 的后代),是所有验证者目标投票中的最高检查点。
令 $c$ 为从 $a$ 延伸到 Epoch $h(b)+1$ 的链上的一个检查点。所有验证者都可以对链接 $a → c$ 进行投票,而不必担心被罚没,因为:
1) 这不会是双重投票。因为没有验证者以 $h(c)$ 为目标进行过投票。 2) 这不会是包围投票。因为诚实验证者不能使用高于 $h(a)$ 的源进行投票,所以 $a → c$ 不会包围别的链接;而因为没有现有链接的目标高于 $h(b)$,所以 $a → c$ 也不会是被包围链接。
 对链接 $a → c$ 进行投票是安全的,既不会是双重投票,也不会是包围投票
对链接 $a → c$ 进行投票是安全的,既不会是双重投票,也不会是包围投票
因此,可以合理化检查点 $c$。随后,对于所有验证者来说为 $c → d$ 投票就是安全的,其中 $d$ 是 $c$ 的直接孩子。由此即可最终化 $c$ 而不会违反守则。
Casper FFG 的分叉选择规则正是基于这种对可信赖活性的需求:底层共识机制必须遵循包含最高合理化检查点的链。根据此证明,只要底层链继续在最高合理化检查点之上构建,我们就可以保证在该链上继续最终化检查点,且不会有人被罚没。
其他
动态验证者集
在以上所有讨论中,我们都假设没有验证者加入或退出协议,从而将 Casper FFG 放在静态验证者集的环境下讨论。但现实中应当允许质押者的假如和退出。
Casper FFG 论文讨论了当验证者集逐个 Epoch 变化时如何保持可问责安全性。文章通过前后验证者集进行了分析。以太坊 2.0 的实现忽略了这一机制,而是对验证者的激活和退出进行了严格限制。每个 Epoch,允许激活和停用的验证者数量大约占全部验证者集的 0.0015%(参见 CHURN_LIMIT_QUOTIENT)。
Gasper 论文中对这一简化进行了分析。通过限制进入和退出率,不考虑前后验证者集,会稍微降低可问责安全性的水平。也就是说,在最终化冲突检查点时,被罚没的权益可能略少于三分之一。具体而言,如果两个冲突的最终化检查点所属 Epoch 的验证者集在权益上相差 $ε$,那么经济最终性(将被罚没的最低权益量)变为 $\frac{1}{3}- ε$,而非 $\frac{1}{3}$。在实践中,验证者集变化率限制非常严格,差异可以忽略不计。
k-最终性
原始的 Casper 论文要求,要最终化一个检查点,从该检查点到其直接子孙节点间必须有绝对多数链接。事实证明,我们可以推广这一点,而不影响安全证明的有效性。
安全证明依赖的关键观察:集合 $B$ 的两个连续成员之间存在绝对多数链接,跨越最终化 $a_m$ 的绝对多数链接 $a_m → a_{m+1}$。
而如果存在绝对多数链接 $a_m → a_{m+k}$,且 $a_m$ 和 $a_{m+k}$ 之间的所有检查点都在 $a$ 分支上被合理化,那么 $b$ 分支上的包围链接仍必定存在。因为这种情况下,$B$ 在 Epoch $m$ 到 $m+k$ 中都不能有成员。
 如果一个绝对多数链接仅跳过合理化检查点,那么可问责安全证明的所有保证都可以保留。这里 $a_5$ 和 $a_6$ 是合理化的,因此可以使用绝对多数链接 $a_4 → a_7$ 安全地最终化 $a_4$
如果一个绝对多数链接仅跳过合理化检查点,那么可问责安全证明的所有保证都可以保留。这里 $a_5$ 和 $a_6$ 是合理化的,因此可以使用绝对多数链接 $a_4 → a_7$ 安全地最终化 $a_4$
因此,推广后的最终性规则是:当有绝对多数链接 $a_m → a_{m+k}$,且检查点 $a_{m+1}, a_{m+2},\dots, a_{m+k-1}$ 都已合理化时,即可最终化检查点 $a_m$。
这就是 k-最终性 (k-Finality),Gasper 论文的 4.5 节对其进行了讨论。
在计算最终性时要考虑多少个检查点 $k$ 取决于想保留多少记录。以太坊 2.0 信标链采用了 2-最终性:记录四个连续 Epoch 的合理化状态,并允许处理两个 Epoch 的目标投票。
 2-最终性的四种情况。在每种情况下,绝对多数链接都会使其源检查点被最终化,并使其目标检查点被合理化。情况 2 和 4 是经典的 1-最终性。
2-最终性的四种情况。在每种情况下,绝对多数链接都会使其源检查点被最终化,并使其目标检查点被合理化。情况 2 和 4 是经典的 1-最终性。
绝大多数时候都只会见到 1-最终性情况,尤其是情况 4。2-最终性仅在大量见证延迟或接近三分之二参与度阈值的时才会发生。
此操作的详细机制在 Epoch 处理期间由 weigh_justification_and_finalization() 函数执行:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def weigh_justification_and_finalization(state: BeaconState,
total_active_balance: Gwei,
previous_epoch_target_balance: Gwei,
current_epoch_target_balance: Gwei) -> None:
previous_epoch = get_previous_epoch(state)
current_epoch = get_current_epoch(state)
old_previous_justified_checkpoint = state.previous_justified_checkpoint
old_current_justified_checkpoint = state.current_justified_checkpoint
# Process justifications
state.previous_justified_checkpoint = state.current_justified_checkpoint
state.justification_bits[1:] = state.justification_bits[:JUSTIFICATION_BITS_LENGTH - 1]
state.justification_bits[0] = 0b0
if previous_epoch_target_balance * 3 >= total_active_balance * 2:
state.current_justified_checkpoint = Checkpoint(epoch=previous_epoch,
root=get_block_root(state, previous_epoch))
state.justification_bits[1] = 0b1
if current_epoch_target_balance * 3 >= total_active_balance * 2:
state.current_justified_checkpoint = Checkpoint(epoch=current_epoch,
root=get_block_root(state, current_epoch))
state.justification_bits[0] = 0b1
# Process finalizations
bits = state.justification_bits
# The 2nd/3rd/4th most recent epochs are justified, the 2nd using the 4th as source
if all(bits[1:4]) and old_previous_justified_checkpoint.epoch + 3 == current_epoch:
state.finalized_checkpoint = old_previous_justified_checkpoint
# The 2nd/3rd most recent epochs are justified, the 2nd using the 3rd as source
if all(bits[1:3]) and old_previous_justified_checkpoint.epoch + 2 == current_epoch:
state.finalized_checkpoint = old_previous_justified_checkpoint
# The 1st/2nd/3rd most recent epochs are justified, the 1st using the 3rd as source
if all(bits[0:3]) and old_current_justified_checkpoint.epoch + 2 == current_epoch:
state.finalized_checkpoint = old_current_justified_checkpoint
# The 1st/2nd most recent epochs are justified, the 1st using the 2nd as source
if all(bits[0:2]) and old_current_justified_checkpoint.epoch + 1 == current_epoch:
state.finalized_checkpoint = old_current_justified_checkpoint
总结
本文介绍了 Casper FFG 中的术语及核心概念,并对其运行机制、可问责安全性、可信赖活性进行了讲解。后续文章将对结合 LMD GHOST 与 Casper FFG 的 Gasper 协议进行探讨。
Casper FFG 的论文中常用 “dynasty” 一词表示 Epoch,只有少数例外,这两个词其实是一回事。 ↩
这两轮与经典 PBFT 共识中的
PREPARE和COMMIT阶段相对应,而PRE-PREPARE阶段大致相当于 Casper FFG 中将检查点块进行广播。 ↩Lighthouse 团队和 Prysm 团队都开发了罚没检测软件。↩ ↩
截止目前(2023年6月),信标链上质押了 2160 万枚 ETH,因此最终性回滚将导致至少 720 万枚 ETH 被罚没。按当前价格计算,相当于有 137 亿美元的安全预算。↩ ↩


